소수란 1과 자기 자신을 제외한 수로만 나누어 떨어지는 수를 말하는데, 간단한 예를 들어보자면 2는 1과 2로 나누어 떨어지니 소수고, 4는 1,2,4로 1과 4를 제외한 2로도 나누어 떨어지기 때문에 소수가 아니다. 그리고 1은 하나밖에 없기 때문에 역시 소수가 아니다.
알고리즘 문제에서 소수 관련 내용이 나오면 소수의 특징을 가지고 문제를 풀어야 하는데 수 있는데, 단순히 찾는 것만 해결하는 것이 아니라 빠르게 많이 찾아야 하기 때문에 간단한 방법인 브루트 포스(Brute Force) 알고리즘과 에라스토테네스의 체를 이용해서 소수를 찾아보자.
브루트 포스(Brute Force) 알고리즘을 이용한 소수 구하기
// 브루트 포스 알고리즘을 이용한 소수 구하기 (시간 복잡도 O(√n))
public static int byBruteForce(int num) {
int[] arr = new int[num+1];
for(int i = 2; i<arr.length; i++) { // num 까지의 수를 배열에 넣고 true 선언
arr[i] = 1;
}
for(int i = 2; i<=num; i++) {
int count = 0;
if(arr[i] == 1) { // 소수일 거라고 예상되는 항목만 수행
for (int j = 2; j <= num; j++) {
if (i % j == 0) {
count++;
}
if(count > 1) { // 자기 자신 외에 추가로 나눌 수 있다면 소수 아님
arr[i] = 0;
break;
}
}
}
}
return (int) Arrays.stream(arr).filter(i -> i == 1).count();
}브루트 포스 알고리즘이란 무차별 대입 방식을 말하는데 간단하게 for 문을 두 번 돌리면서 각 수를 2부터 시작해서 숫자 올리면서 나눠본 뒤, 자기 자신으로만 나눌 수 있으면 소수고 그 외에는 소수가 아니기 때문에 한 번만 나눠 떨어지는 값을 찾아주면 되는 식이다. (1은 당연하기 때문에 따로 계산하지 않아도 됨)
이 방법은 수가 작은 경우에는 별 문제가 없지만, 들어오는 숫자 범위가 커지면 커질수록 for 문에서 많은 시간을 허비하기 때문에 대부분의 코딩 테스트에서는 아래의 에라토스테네스의 체를 사용해 줘야 한다.
에라토스테네스의 체를 이용한 소수 구하기
// 에라토스테네스의 체 -> 소수의 제곱은 모두 소수가 아님
public static int byEratosthenes(int num) {
int[] arr = new int[num+1];
for(int i = 2; i<arr.length; i++) { // num 까지의 수를 배열에 넣고 true 선언
arr[i] = 1;
}
int sqrt = (int) Math.sqrt(num);
for(int i = 2; i<=num; i++) {
if(arr[i] == 1) { // 소수일 거라고 예상되는 항목만 수행
for (int j = 2; j <= sqrt; j++) { // 제곱근보다 큰 값은 계산할 필요 없음
if (i % j == 0) {
for(int k = 2; i*k <= num; k++) { // 소수의 제곱은 모두 소수가 아님
arr[i*k] = 0;
}
}
}
}
}
return (int) Arrays.stream(arr).filter(i -> i == 1).count();
}에라토스테네스의 체의 핵심은 소수의 제곱은 모두 소수가 아니라는 내용인데 2는 소수지만 4부터는 1,2,4로 나눠지고 6은 1,2,3,6으로 나눠지기 때문에 소수를 한번 발견한 후 해당 소수의 배수를 모두 제외해주면 소수 하나만 찾아도 해당 소수의 배수는 모두 계산하지 않고 제외할 수 있다.
또한 효율성을 높이기 위해서는 1부터 100까지의 수를 찾아야 한다면 모든 값을 다 찾는 것이 아니라 목표 값의 제곱근까지만 찾아도 되는데, 제곱근은 수를 자신으로 곱한 갑을 말하고 예를 들어보면 9의 제곱근은 3이고, 120의 제곱근은 10.95다(소수점 버림), 여기서 제곱근을 찾으면 1부터 10까지만 찾은 후 배수를 제거하면 소수만 남게 되기에, 1부터 100까지 돌려가며 소수를 찾는 것보다 훨씬 빠르게 처리할 수 있다.
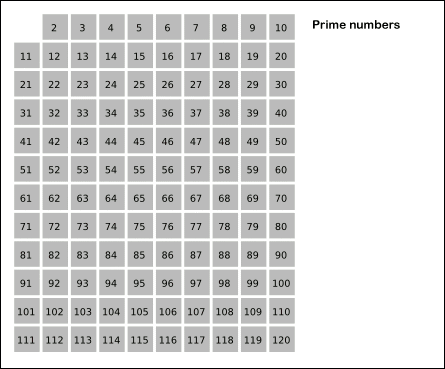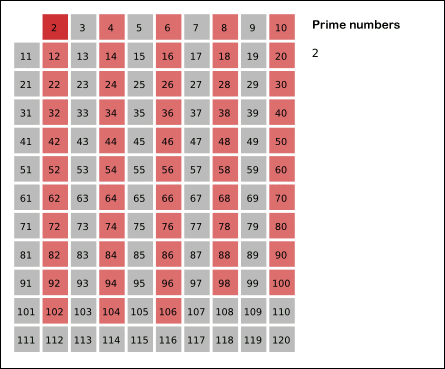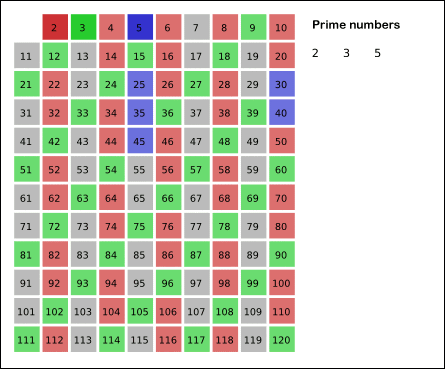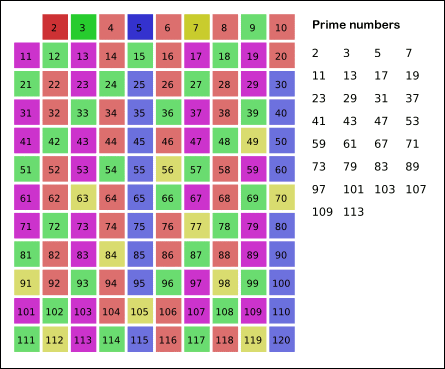
이제 설명을 봤으니 에라토스테네스의 채를 GIF로 보면서 다시 정리해보면, 소수를 찾은 뒤 소수의 배수를 모두 제외하되, 1부터 120까지 모두 진행할 필요 없이 120의 제곱근인 10까지만 진행해도 배수 빼내는 과정에서 소수가 아닌 값은 다 빠지게 되므로, 빠르게 소수인 숫자들만 찾아줄 수 있다.

Leave a Reply