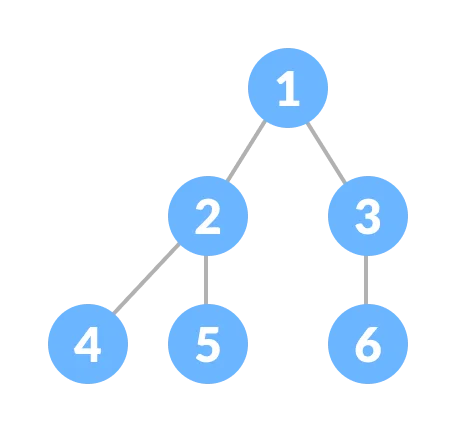
우선순위 큐(Priority Queue)를 알기 전에 힙(Heap)에 대해 알 필요가 있는데, 힙은 완전 이진 트리 구조를 가진 자료구조로 완전 이진 트리를 읽는 순간 뇌에 혼란이 오면서 이게 대체 무슨 말인가, 그냥 뒤로 가기 눌러야 되나 이런 생각이 들 텐데 뒤로 가기를 누르기 전에 아래로 내려가 이미지를 보면

이미지 출처 : https://www.programiz.com/dsa/complete-binary-tree

노드가 모든 레벨(줄)에서 완전히 채워져 있거나 마지막 레벨을 제외한 모든 레벨이 채워져 있는 구조인 것이 보일텐데, 값이 들어오면 마지막 레벨 기준 왼쪽에서 오른쪽으로 들어가게 된다, 여기에 값 또한 정렬된 상태인 것이 보일텐데, 완전 이진 트리 구조란 부모 노드(특정 노드 기준 위에 있는 값)의 값이 항상 크거나 같게 / 작거나 같게 정렬되는 구조로 값을 추가하면 트리의 가장 마지막 위치에 삽입되면서 부모 노드와 비교 후 위치를 바꾸는 정렬을 수행하고 되고 이 정렬은 값을 계속 비교하면서 값에 따라 루트 노드까지 도달하게 된다, 반면 값이 삭제될 경우에는 루트 노드의 값을 삭제하되 자식 노드를 부모 위치로 올려주면서 트리 구조를 유지하게 된다.

들어도 여전히 뭔 말인지 이해가 안될 경우 실제 그림을 그려야 하는 것은 아니므로 압축을 해 보자면 Queue에 값을 넣거나 빼면 자동 정렬이 진행되고 삽입/삭제/조회 시 시간 복잡도는 O(log n)인 형태가 되겠다. 이제 힙 개념이 정리되었다면 우선순위 큐는 힙을 사용해 구현한 큐라고 이해하면 되겠다!

PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(); // 오름차순
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(Collections.reverseOrder()); // 내림차순

하지만 여전히 뒤로 가기를 누르고 싶다면 그림은 제껴 놓고 코드로 보자면 PriorityQueue를 선언한 후 값을 넣어주기 시작하면 값을 넣는 동시에 오름차순(작은 값이 위로), 내림차순이 자동으로 진행되는 Queue를 사용할 수 있게 되고, O(log n)의 시간 복잡도란 들어오는 양이 매우 큰 경우에도 반으로 쪼개면서 범위를 줄여나가므로 효율적인 성능을 보장하지만 단순 List 값 넣고 정렬했다면 모든 값을 순차 비교하기 때문에 들어오는 양이 많아질수록 비효율적이게 된다. 반면 들어오는 데이터가 작은 경우에는 위의 단순한 방법보다 훨씬 느리게 동작하게 된다.

결국 우선순위 큐(Priority Queue)는 힙을 이용해 데이터를 우선순위 순으로 정렬하여 저장하는 자료구조를 말하는데 마지막으로 특징을 간략하게 요약을 해 보자면 아래 내용이 되겠다.

• 데이터는 우선순위 순으로 정렬되어 저장
• 가장 우선순위가 높은 데이터가 먼저 처리됨
• 삽입, 삭제, 조회 연산을 모두 O(log n)의 시간 복잡도로 수행 가능
  • 들어오는 데이터가 많을 경우 효율적인 성능 보장, 반대의 경우에는 비효율